Стоимость практических пособий
| Пантограф «Фибоначчи» | 11 000 руб. |
| Разметчик «Фибоначчи» | 11 000 руб. |
| Инверсор «Фибоначчи» | 11 000 руб. |
| Трисектор «Фибоначчи» | 11 000 руб. |
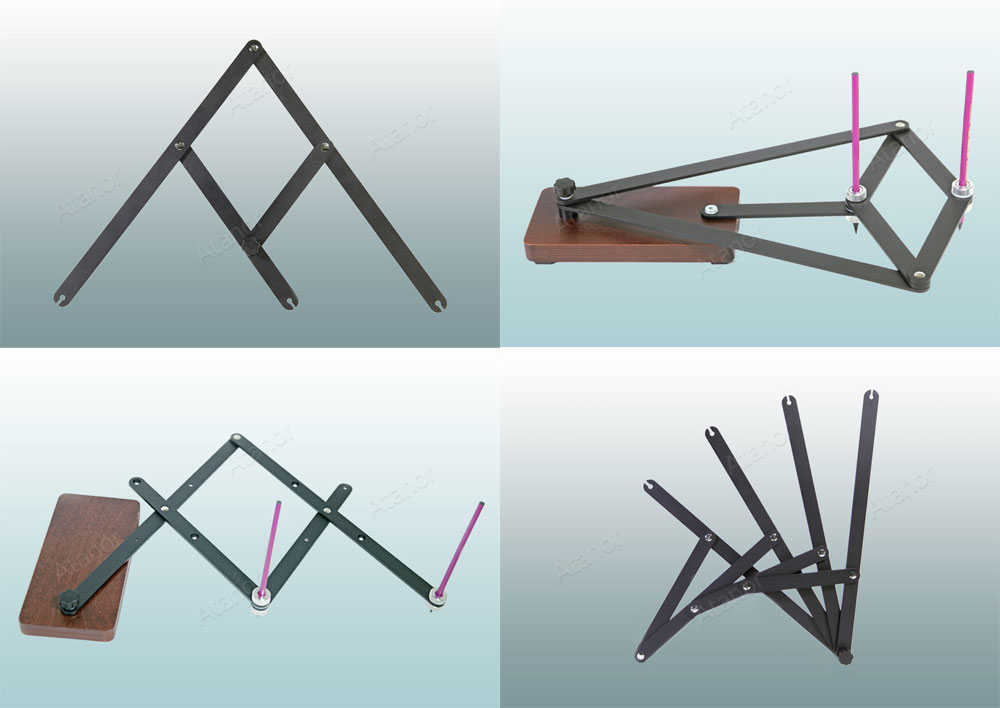
Пантограф «Фибоначчи»
Занимательная геометрия. Простые вещи, пробуждающие интерес и помогающие научиться новому.
Что может пантограф?
Пантограф «Фибоначчи» в простой и увлекательной форме знакомит детей с преобразованиями подобия (гомотетией).
Пантограф предоставляет возможность вычертить фигуру, перспективно-подобную любой заданной фигуре.
Отлично развивает уровень пространственного воображения и логики.
Пробуждает интерес к учебе. Гомотетия и ее математические законы позволяют найти оригинальное и красивое решение для многих задач, где использование традиционных методов будет громоздким и потребует много времени.
Для преподавателей и учеников
Пантограф «Фибоначчи» может быть использован во время обычного урока геометрии как иллюстрация при объяснении темы преобразований подобия, на дополнительных или углубленных занятиях. А также на занятиях по естествознанию, рисованию.
Интересные факты о пантографе и преобразованиях подобия
Первый пантограф был создан вначале 17 века немецким математиком, астрономом, физиком и механиком Кристофом Шейнером.
Принцип работы пантографа (изменение размера с сохранением пропорций) позволяют этому термину использоваться в самых различных областях человеческой деятельности.
Еще совсем недавно пантографы широко использовались в черчении для перечерчивания планов, карт, крупных схем в более мелком масштабе.
Принцип преобразования подобия использовался еще при создании фотографии и до сих пор используется в получении видеопроекций в изобразительном искусстве.
Пантограф на старом рисунке
Разметчик «Фибоначчи»
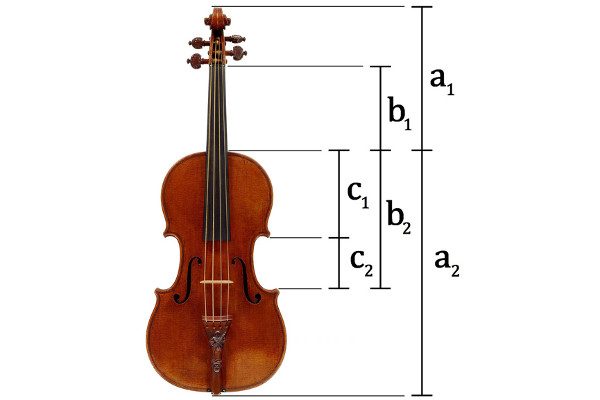
Разметчик «Фибоначчи» предназначен для деления отрезка в пропорции «золотого сечения». Понятный практический инструмент при изучении темы золотого сечения и гармонических пропорций в окружающем мире.
Интересно и наглядно. В помощь педагогу
Тема золотого сечения в окружающем нас мире — одна из интереснейших в курсе геометрии. С помощью разметчика «Фибоначчи» учащиеся получают возможность не только послушать рассказ учителя или посмотреть презентацию, но и убедиться в этих законах лично: быстро и просто измерить пропорции античного храма на фотографии или пропорции фаланг пальцев собственной руки.
Развитие интереса к предмету и творческого мышления
На примере золотого сечения и разметчика Фибоначчи можно показать, как используются законы математики в современном мире и как они могут оказаться полезными в будущей профессии:
- пропорции многих видов современной мебели основаны на законе золотого сечения, в чем можно просто убедиться, замерив их размеры;
- пропорции многих музыкальных инструментов также основаны на золотом сечении.
Скрипка. Пропорции золотого сечения
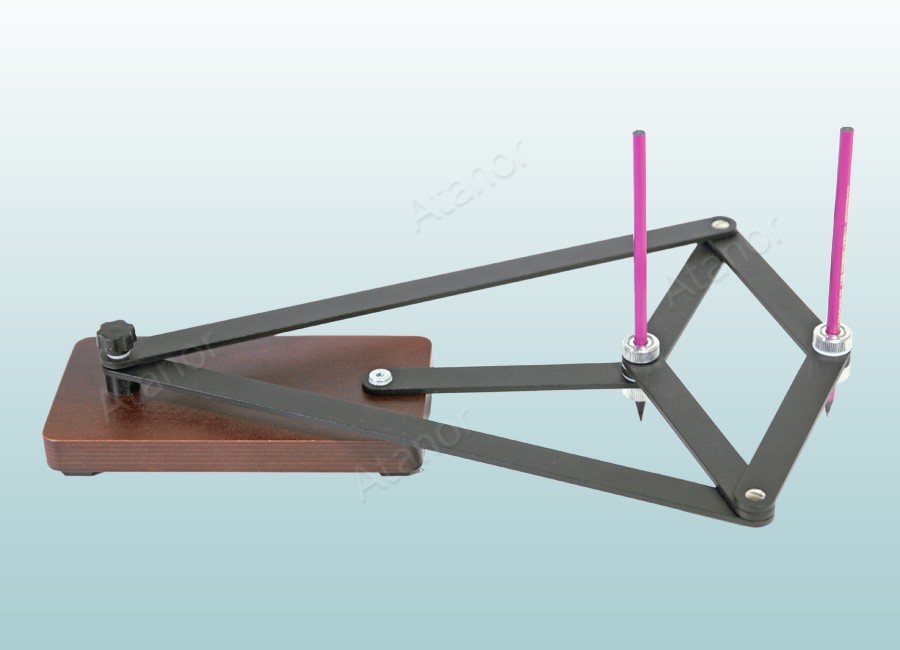
Инверсор «Фибоначчи»
Инверсор «Фибоначчи» предназначен для демонстрации геометрического преобразования «Инверсия».
Инверсор «Фибоначчи» позволяет без дополнительных вычислений вычертить линию, инверсную любой данной линии.
Немного об инверсорах
Инверсор «Фибоначчи» воспроизводит механизм Поселье-Липкина, ставший первым инверсором, позволяющим преобразовывать прямолинейное движение в движение по окружности и наоборот.
Со времен изобретения паровой машины перед конструкторами и инженерами остро встала задача построения шарнирного механизма, способного преобразовывать движение одного шарнира по окружности в прямолинейное движение другого шарнира (и обратно). Решение задачи было найдено в области математики. Им и стал инвертор Поселье-Липкина.
С помощью усложненной версии инверсора Поселье-Липкина можно построить механизмы для извлечения квадратных и кубических корней, деления угла на три части и др.
Занимательная математика и механика
Инверсор, пантограф, разметчик и трисектор «Фибоначчи» будут отличными практическими инструментами для математического класса, для дополнительных занятий и олимпиад.
На примере этих простых и гениальных инструментов учащиеся видят, как сухие формулы и теории находят красивое, практическое применение. Таким образом, они учатся мыслить нестандартно, и это пробуждает в них тягу к углубленному изучению предмета.
Трисектор на антипараллелограммах
Трисектор служит для разделения выбранного угла на три равные части.
Нестандартные решения для вечных задач
Задача о разделении угла на три равные части (трисекция угла), вместе с задачами о квадратуре круга и удвоением куба, пришла к нам из Древней Греции. Долгое время ее пытались решить с помощью циркуля и линейки, пока не было доказано, что это невозможно.
Возможно, что именно задача трисекции угла послужила толчком к поиску нестандартных решений задач по механике и математике.
Задача легко решается практическим способом с использованием наглядного пособия «Трисектор на антипараллелограммах».
Для школьников 7-11 классов и углубленного изучения
Для лабораторий математики и математических классов в качестве дополнительного учебного материала. Для школьников 7 — 11 классов.
Наглядное практическое пособие по математике
Вместе с другими практическими пособиями (пантограф, разметчик и инверсор) служат отличным материалом для таких занятий, как «Плоские шарнирные механизмы», «Принципы подобия», «Математика и история технологий».
